TRABAJO DE GEOMETRÍA

1. El triángulo
1.1 Propiedades y tipos de triángulos 

Propiedades:
  1. Un lado de un triángulo es menor que la suma de los otros dos y mayor que su diferencia.                 
2. La suma de los ángulos interiores de un triángulo es igual a 180°.
3. El valor de un ángulo exterior es igual a la suma de los dos interiores no adyacentes.

1 Según sus lados
                                               
                                            Triángulo equilátero

                                                 Tres lados iguales
 
                                                    
                                            Triángulo isósceles 

                                               Dos lados iguales


                                             
                                         Triángulo escaleno
                                         Tres lados desiguales.


2. Según sus ángulos.

                                          
                                     Triángulo acutángulo

                                       Tres ángulos agudos.


                                              
                                   Triángulo rectángulo

                                         
Un ángulo recto. El lado mayor es la hipotenusa. 

Los lados menores son los catetos. 

                                 

                                        
                             Triángulo obtusángulo

                                  Un ángulo obtuso.

   

1.2 Rectas y puntos notables en el triángulo (http://gaussianos.com/los-centros-del-trianguloincentro-baricentro-circuncentro-y-ortocentro/) 


BARICENTRO: Es el centro de gravedad del triángulo. Cada mediana divide al triángulo en dos triángulos de igual área. Además el baricentro dista doble del vértice que del punto medio del lado.

CIRCUNCENTRO: El punto O donde se cortan las tres mediatrices se llama Circuncentro y equidista, es decir, está la misma distancia de los tres vértices A, B y C, es por eso que pertenece a las tres mediatrices. 


ORTOCENTRO: En un triángulo ABC, las tres alturas se cruzan en un punto llamado Ortocentro. Se puede ver que si trazamos por cada vértice una paralela al lado opuesto se obtiene otro triángulo cuyas mediatrices son justamente las alturas del triángulo primitivo.

INCENTRO: El punto I donde se cortan las tres bisectrices interiores se llama Incentro, equidista de los tres lados y por eso podemos construir una circunferencia de centro I tangente a los lados del triángulo.



1.3 El teorema de Pitágoras 

1.3.1 Demostración gráfica. 

1.3.2 El teorema en 3D 

1.4 El teorema de Tales , triángulos semejantes. ¿Cómo calcular la altura de un árbol a partir de su sombra? 
1. Primero medimos la sombra del árbol

2. Luego medimos nuestra altura, y la longitud de nuestra sombra

3. Realizamos los cálculos:
1.60 / 1.10 x 1.90 = 2.76 m
Conclusiones
El teorema de tales es muy efectivo para resolver problemas matemáticos de una forma más rápida y efectiva. Podemos medir cualquier objeto cuando el sol proyecta su sombra, medimos su longitud y la nuestra y luego solo aplicamos la fórmula.
2. Lugares geométricos 
2.1 ¿Qué es un lugar geométrico?
 Es un conjunto de puntos que satisfacen determinadas condiciones o propiedades geométricas.
2.2 La mediatriz y la bisectriz 
Mediatriz:
Definición: Lugar geométrico de los puntos del plano que equidistan de los extremos de un segmento.




Propiedades:  

• Las distancias AO y BO son iguales.
• Toda circunferencia con centro en un punto de la mediatriz que pase por uno de los extremos del segmento pasará también por el otro.
• A y B son simétricos con respecto a la mediatriz.  

Bisectriz:

Definición: Lugar geométrico de los puntos del plano que equidistan de las semirrectas que forman el ángulo.

Propiedades:

• Las distancias PA y PA' son iguales.
• Una circunferencia con centro en P que pase por A, también pasará por A' y será tangente a los lados del ángulo.
• Los lados del ángulo son simétricos con respecto a la bisectriz.

2.3 Las cónicas 
2.3.1 ¿Qué es una cónica? 
 Es el lugar geométrico de los puntos del plano (x,y) que satisfacen una ecuación completa de segundo grado:

Bx^2 + Cy^2 + Dxy + Fx + Gy + H=0
2.3.2 La circunferencia 
 Lugar geométrico de los puntos del plano que equidistan de un punto fijo llamado centro. El radio de la circunferencia es la distancia de un punto cualquiera de dicha circunferencia al centro.

 β = 90º
La circunferencia es un caso particular de elipse.

2.3.3 La elipse: 
Es la sección producida en una superficie cónica de revolución por un plano oblicuo al eje, que no sea paralelo a la generatriz y que forme con el mismo un ángulo mayor que el que forman eje y generatriz.

     α < β <90º

La elipse es una curva cerrada.
                                            
 Obtención en un cono: 
                                          
 Método del jardinero:
                                          
 Mesa de billar elíptica:
                                          
 2.3.4 La hipérbola: 
Es una sección cónica, una curva abierta de dos ramas obtenida cortando un cono recto por un plano oblicuo al eje de simetría, y con ángulo menor que el de la generatriz respecto del eje de revolución.
 Obtención en un cono 
                                                                  
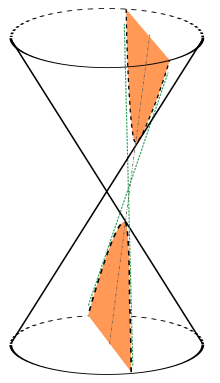
 La lámpara hiperbólica
                                                    
2.3.5 La parábola: 
 Es la sección cónica de excentricidad igual a 1, resultante de cortar un cono recto con un plano cuyo ángulo de inclinación respecto al eje de revolución del cono sea igual al presentado por su generatriz.
 Obtención en un cono 
                                                    
 La antena parabólica
                                         
 El horno solar
                                     
 El espejo parabólico 
                                         
3. Movimientos en el plano
3.1 Las traslaciones. ¿Qué es un vector?
Segmento de recta, contado a partir de un punto del espacio, cuya longitud representa a escala una magnitud, en una dirección determinada y en uno de sus sentidos.
3.2 Ejercicios de vectores y translación
3.2.1 Dados los vectores u=(4,3) y v=(-1,4), hallar: 
a) su representación gráfica en un sistema de coordenadas
b) los vectores u + v  y u - v por la regla del paralelogramo 
c) las componentes de los vectores anteriores 

d) el módulo de cada uno de los vectores  

3.2.2 Dibuja las figuras trasladadas de las siguientes en una traslación de vector guía u(4,3):
                                     

                                     

                                      

                                       
3.4 Simetría. Ejercicios
3.4.1 Dado el triángulo de vértices A(-2,2), B(6,-1) y C(7,5) se pide: a) dibujar el triángulo b) hallar el triángulo simétrico respecto del centro de simetría O(0,0) c) hallar el triángulo simétrico respecto del eje OX

3.4.2 Euclides (aproximadamente 300 a. C.) enunció las leyes de reflexión de la luz sobre un espejo plano. Herón de Alejandría, 400 años después, afirmó algo más sencillo: "La luz ha de tomar siempre el camino más corto". Sirviéndote de esta idea, halla en que punto del espejo se ha de reflejar un rayo de luz que parte del punto A para que después llegue a B.
 
3.4.3 Carlos y Fernando están jugando al billar. En un determinado momento las bolas se encuentran en las posiciones indicadas por el dibujo. Indica el camino que debe seguir la bola A para que rebotando en la banda MQ golpee a la bola B.

Indica el camino que debe seguir la bola A para que rebotando en la banda NP y PQ golpee a la bola B.


3.5 Frisos, mosaicos y cenefas 

Un friso o cenefa es la aplicación de una traslación a una misma figura de manera sucesiva. Esta aplicación forma un mosaico.

3.6 MC. Escher
Es un artista nacido en 1898, en los Países Bajos. Se caracteriza por hacer grabados y obras cuyas formas son imposibles. Crea cuadros de color sepia y en blanco y negro, y juega con las formas engañando al cerebro humano. Sus obras más importantes son:
1. DROWING HANDS
                                     
2. RELATIVITY
                                     
3. DAY AND NIGHT
                                     
4. Áreas y volúmenes de figuras conocidas.


5. La esfera y el globo terráqueo 
5.1 Elementos principales de la esfera. 
Centro:Punto interior que equidista de cualquier punto de la esfera.
Radio: Distancia del centro a un punto de la esfera.
Cuerda: Segmento que une dos puntos de la superficie.
Diámetro: Cuerda que pasa por el centro.

Polos: Son los puntos del eje de giro que quedan sobre la superficie esférica.
5.2 Elementos de la esfera terrestre. 
Los paralelos son circunferencias perpendiculares al eje terrestre, con orientación este-oeste, que dependiendo de su ubicación tienen una extensión variable. La línea del Ecuador o paralelo cero grados, llamado también de origen o referencia, es el de mayor extensión, divide a la Tierra en dos hemisferios: el Norte o Septentrional y el Sur o Austral. A partir del Ecuador, se establecieron 90 grados hasta el polo norte y 90 grados hasta el polo sur.


Los meridianos son semicircunferencias que comienzan y terminan en los polos, es decir tienen orientación norte-sur. En 1884, se determinó que el meridiano cero grados o de origen es el que pasa por el observatorio astronómico de la ciudad de Greenwich, cerca de Londres, dividiendo el planeta en los hemisferios: Occidental u Oeste y Oriental o Este.

La latitud es la distancia de un lugar con relación al paralelo del Ecuador o 0°. Como los paralelos están en grados, la latitud también lo está. El polo norte tiene una latitud de 90¼ norte, mientras el polo sur está en la latitud 90¼ sur.

 La longitud es la distancia que separa un punto determinado del globo del meridiano de Greenwich. Al igual que los meridianos, la longitud también se mide en grados, puede ser hasta de 180° este o 180° oeste.
                                      
5.3 Los husos horarios, la hora local solar y oficial. 
En geografía, huso horario es cada una de las veinticuatro áreas en que se divide la Tierra, siguiendo la misma definición de tiempo cronométrico. Se llaman así porque tienen forma de huso de hilar, y están centrados en meridianos de una longitud que es un múltiplo de 15°. Anteriormente, se usaba el tiempo solar aparente, con lo que la diferencia de hora entre una ciudad y otra era de unos pocos minutos en el caso de que las ciudades comparadas no se encontraran sobre un mismo meridiano. El empleo de los husos horarios corrigió el problema parcialmente, al sincronizar los relojes de una región al mismo tiempo solar medio.
Todos los husos horarios se definen en relación con el denominado tiempo universal coordinado (UTC), huso horario centrado sobre el meridiano de Greenwich que recibe ese nombre por pasar por el observatorio de Greenwich (Londres).

Puesto que la Tierra gira de oeste a este, al pasar de un huso horario a otro en dirección este hay que sumar una hora. Por el contrario, al pasar de este a oeste hay que restar una hora. El meridiano de 180°, conocido como línea internacional de cambio de fecha, marca el cambio de día.

5.4 El método de Eratóstenes para calcular el diámetro de la circunferencia terrestre

                                  

FUNCIONES

1 ª PARTE: Conceptos básicos 
1. ¿Cómo puedes expresar la relación entre dos magnitudes como, por ejemplo, la masa y el volumen de un cuerpo? 
 La masa es físicamente la materia que posee un cuerpo: átomos, moléculas, espacios, elementos,...
El espacio que una masa ocupa en un cuerpo.
La relación que tienen entre si es directamente proporcional: A mayor cantidad de masa, mayor es el volumen
La densidad es la relación entra la masa y el volumen.. 
si tenes + masa en igual volumen, la densidad es mayor 
si tenes - masa en igual volumen, la densidad es menor 
si tenes - densidad en igual masa, significa que el volumen mayor 
si tenes + densidad en igual masa, el volumen es menor 
2. ¿Qué es una función? ¿De qué formas pueden expresarse las relaciones entre magnitudes? Pon ejemplos de funciones de la vida cotidiana; puedes buscar en revistas, periódicos, etc. En las figuras siguientes tienes 3 ejemplos:
Es una relación entre un conjunto dado X (llamado dominio) y otro conjunto de elementos Y (llamadocodominio) de forma que a cada elemento x del dominio le corresponde un único elemento f(x) del codominio (los que forman el recorrido, también llamado rango o ámbito). Se pueden expresar mediante: fórmulas, tablas, gráficos y el lenguaje.
Algunos ejemplos de la vida cotidiana son: peso/precio, cantidad/precio, espacio/tiempo.
                                    
3. ¿Qué es la tasa de variación de una función? ¿Qué valores toma para las funciones crecientes y decrecientes? Puedes utilizar ejemplos gráficos para responder.
Es la diferencia entre las ordenadas correspondientes a los puntos de abscisas a y a+h.
Funciones crecientes: Son cada vez mayores a medida que aumentan los valores de la variable x. Funciones decrecientes: Son cada vez menores a medida que aumentan los valores de la variable x
                                 
4. Utilizando la representación gráfica de una o varias funciones, explica las diferencias entre máximos y mínimos absolutos y relativos. 
Un máximo absoluto es aquel que  la ordenada es mayor o igual que en cualquier otro punto del dominio de la función, mientras que el mínimo absoluto es aquel que la ordenada es menor o igual que en cualquier otro punto del dominio de la función.
  

Un máximo relativo es aquel que f (b) es mayor o igual que los puntos próximos al punto a, mientras que un mínimo relativo es aquel que  f (b) es menor o igual que los puntos próximos al punto b.

a = 3.08     b = -3.08

5. Representa gráficamente dos ejemplos de funciones simétricas respecto al eje de ordenadas (eje y) y respecto al origen (0,0). Explica en qué consiste cada tipo de simetría. 




 6. Representa gráficamente una función periódica indicando por qué se denomina de esa forma. 

sen(x)
Se denomina así debido a que la forma de la línea se repite de forma periódica, es decir, se repite constantemente.

7. Pon dos ejemplos, uno de función continua y otro de función discontinua. ¿Cuál es la diferencia entre ambas? 
Para que una función sea continua se deben cumplir 3 condiciones 
1-tanto su limite lateral por la izquierda como por la derecha deben ser iguales 
2- ademas la función debe estar definida en dicho punto de análisis 
3- tanto el paso 1 y el paso 2 deben ser iguales 
Si no cumple con una de las 3 condiciones se dice que es discontinua en ese punto.
Ejemplos:


8. Investiga: ¿Cuál es el origen del término función? 

Nació ligado a la idea de dependencia de cantidades variables, en unión al estudio del movimiento, en época de Galileo Galilei, y con la caracterización dada por Nicolás de Oresme: "Todo lo que varía, se sepa medir o no, lo podemos imaginar como una cantidad continua representada por un segmento". Esta concepción de carácter físico y geométrico antecedió a la noción cartesiana de dependencia numérica.

Este concepto resultó demasiado restrictivo para las necesidades de la física matemática, por lo que la idea de función debió pasar por un largo proceso de generalización y clarificación.

9. Representa gráficamente las funciones que se proponen indicando sus propiedades. Elabora una tabla resumen con todas las gráficas obtenidas. 

 Función lineal creciente: 

                                                                    y= x+2

Función lineal constante: 

y=69

 Función lineal decreciente:

y=-x+2

Rectas paralelas:

                                                      y=2x+1        y=2x+2

 Función cuadrática cóncava: 

                                                

y=-x^2+20x
Función cuadrática convexa: 

                                                  y= 0.25x^2 + 8
g) Investiga sobre la representación gráfica de otras funciones:

y=x sen(x)

y=-x sen(x)

10. Investiga sobre la representación de funciones en coordenadas polares. 
El sistema de coordenadas polares es un sistema bidimensional. En él, cada punto está determinado por un ángulo y una distancia. Guarda un cierto parecido con el sistema de coordenadas cartesianas. Se llama x a la distancia entre el punto central y el punto en el plano (P). Uno de sus usos es en la navegación, pero uno de los más interesantes es la creación de figuras.




 11.Utilizando uno de los programas anteriores investiga sobre la representación gráfica de funciones en el espacio (x, y, z).

12.Utiliza el programa que has elegido para resolver gráficamente el sistema de dos ecuaciones lineales con dos incógnitas siguiente: 

3x - 2y= 4

2x + 3y= 33

13.Elige un modelo de coche que disponga de motorizaciones diesel y gasolina y realiza un estudio gráfico de la función coste que nos permita averiguar cual es el automóvil más adecuado para nosotros en función del número de kilómetros que recorremos anualmente. (Nota: Necesitas el precio del coche, el del combustible y el consumo combinado) 

                                   Modelo Gasolina                                  Modelo Diésel

Precio                                     25000,00                                            8200,00

Consumo 4x100km                      6,9                                                        5,2

Coste/Km                                  0,090735                                            0,0507

Expresión                              Y=25000+0.090735x               Y= 28200+0.0507x

14.Interpreta la gráfica del recorrido del Maratón Popular de Madrid
La salida se encuentra a 640m y van subiendo hasta 720m en 5 minutos, despues descienden hasta 680m donde se mantiene constante hasta los 10 minutos, a partir de los 10 minutos empieza otra vez a descender hasta situarse por los 640m aprox y se mantiene hasta los 15 minutos, sube hasta los 720m en el minuto 25 luego vuelve a bajar hasta los 680 y luego vuelve a subir hasta los 720m en el minuto 35 aprox.despues se mantiene en los 680m hasta que llega a la meta.